SOLICITUD DE ADMISIÓN
Fecha límite de registro 24 de agosto
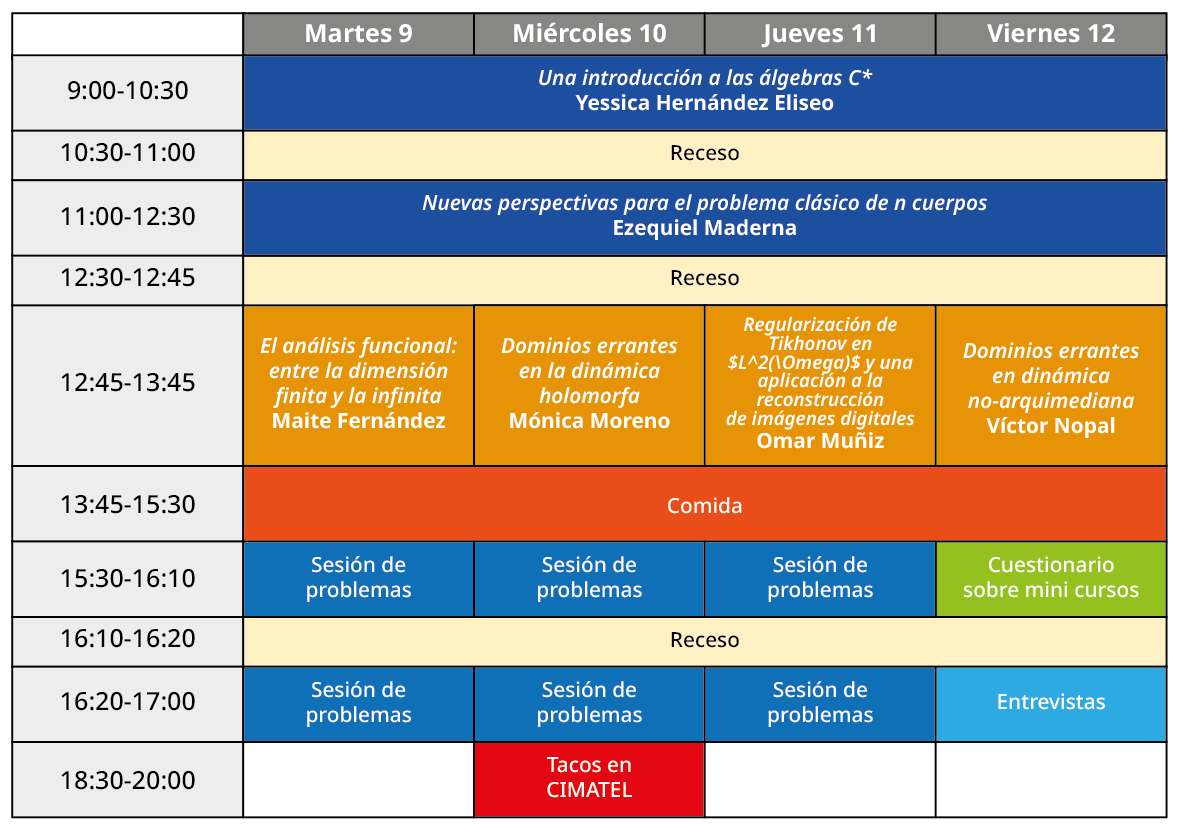
CURSOS
Una introducción a las álgebras C*
Yessica Hernández Eliseo
Las álgebras C* son piedra angular del análisis funcional, éstas y las álgebras de von Neumann se consideraron por primera vez en la mecánica cuántica para modelar álgebras de observables físicos. Después, alrededor del año 1947, Israel Gelfand y Mark Naimark desarrollaron una teoría abstracta de las álgebras C*, axiomatizando las propiedades básicas que tienen los operadores en un espacio de Hilbert. Posteriormente, identificaron estas álgebras por su clasificación en conmutativas y no conmutativas. Este curso tiene como objetivo dar a conocer las álgebras C*, veremos algunos ejemplos que nos permitan interpretar los resultados que abordaremos en el curso. Nos enfocaremos en álgebras C* con unidad, primero veremos propiedades del espectro de los elementos de estas álgebras. Posteriormente, usando la transformada de Gelfand, identificaremos las álgebras C* abelianas con álgebras C* de funciones continuas sobre un espacio compacto Hausdorff. Siguiendo esta idea y usando teoría de representaciones, enunciaremos el teorema de Gelfand-Naimark-Siegal, el cual identifica las álgebras C* no abelianas como subálgebras C* de operadores en un espacio de Hilbert.
Requisitos: haber cursado la asignatura de Álgebra Lineal. Estar familiarizado con el análisis funcional, y con algunos conceptos básicos de topología.
Referencias
- G. R. Douglas, Banach Algebra Techniques in Operator Theory Academic Press, New York and London, 1972.
- K. Zhu, An introduction to operator algebras. CRC Press, Florida, 1993.
- G. J. Murphy, C* Algebras and Operator Theory. Academic Press, New York, 1990.
Nuevas perspectivas para el problema clásico de n cuerpos
Ezequiel Maderna
El modelo newtoniano para la gravitación es considerado como una de las mayores revoluciones científicas de la historia, ya que logró explicar -- de forma unificada -- muchos fenómenos físicos a escala terrestre así como el movimiento de los planetas de nuestro Sistema Solar (mecánica celeste). Si bien el surgimiento de la teoría de la relatividad general ha refinado el modelo newtoniano, éste sigue siendo absolutamente satisfactorio para las aplicaciones tecnológicas actuales o análisis astronómico (diseño y control de órbitas de satélites artificiales, estaciones espaciales o telescopios, predicción de colisiones de meteoritos, evolución final y comprensión de la formación de nuestro sistema así como de exoplanetas, etc). Este curso no tratará las aplicaciones, sino que se centrará en el modelo matemático en sí mismo, al cual han aportado a lo largo de la historia muchos de los grandes matemáticos, no siempre con éxito pero construyendo nuevas teorías matemáticas, como por ejemplo el comienzo de la teoría moderna de los Sistemas Dinámicos a partir de los trabajos de Poincaré, desarrollo de la teoría KAM en la segunda mitad del siglo XX. Vamos a introducir los fundamentos de esta teoría clásica, y a presentar algunos de los principales temas de investigación actuales, en particular los que pueden ser abordados mediante técnicas variacionales.
Requisitos: un curso básico de ecuaciones diferenciales. Es de utilidad tener nociones de geometría diferencial y de geometría Riemanniana, pero no son imprescindibles.
Referencias
R. Montgomery, Four Open Questions for the N-Body Problem, Cambridge University Press (2024).
CHARLAS
El análisis funcional: entre la dimensión finita y la infinita
Maite Fernández
S. Banach introdujo la noción de lo que ahora conocemos como espacio de Banach, en 1920, en el contexto de los espacios de funciones, que normalmente son de dimensión infinita. Pero en realidad, la definición no distingue entre espacios de dimensión finita o infinita. Este hecho resulta ser una característica clave en la teoría, que podemos ver reflejada en sus vínculos con distintas áreas de las matemáticas y que, a la vez, enriquecen su propio desarrollo. En esta plática exploraremos cómo se combinan las perspectivas de dimensión finita e infinita, así como algunas consecuencias importantes de esta combinación.
Dominios errantes en la dinámica holomorfa
Mónica Moreno
Considera un endomorfismo f:S->S actuando sobre una superficie de Riemann S. Si U es un subdominio de S donde la familia de iterados restringida a U es normal, entonces decimos que U es una componente de Fatou de f. El objetivo de esta charla es discutir el caso cuando U es una componente errante: esto es, cualquier par de iterados (positivos) de U bajo f tienen intersección vacía. Desde 1920 se conjeturaba que si f es una función racional de grado al menos 2 y S es la esfera de Riemann, entonces no podría tener dominios errantes; Dennis Sullivan demostró en 1984 que la conjetura es cierta. Sin embargo, antes a su demostración ya se conocían ejemplos de funciones meromorfas trascendentes con dominios errantes. Platicaremos sobre la demostración de Sullivan, presentaré algunos ejemplos de funciones meromorfas con dominios errantes y comentaré sobre las líneas de investigación actual relacionadas a este tipo de componentes.
Regularización de Tikhonov en $L^2(\Omega)$ y una aplicación a la reconstrucción de imágenes digitales
Omar Pérez
Consideremos la ecuación lineal $Au+n=v$, donde $A$ es un operador lineal de $L^2(\Omega)$ en sí mismo, $\Omega$ es un subconjunto abierto y acotado del plano con frontera suave, $n,v \in L^2(\Omega)$ y $u$ es la variable desconocida. Los parámetros de $A$ y de $n$ no son conocidos, pero se pueden estimar. Nuestro problema consiste en inferir $u$ disponiendo sólo del dato $v$. Sería deseable que este problema estuviera bien planteado en el sentido de Hadamard, es decir, quisiéramos que su solución $u$ existiera, fuera única y dependiera continuamente de los datos iniciales; pero por lo general no es así. Para transformar este problema en un problema bien planteado se suele recurrir a la técnica de regularización de Tikhonov, que básicamente añade una nueva restricción al problema y lo formula como un problema de minimización de un funcional definido en $L^2(\Omega)$. Este problema de minimización también se puede formular como una EDP elíptica con condición de frontera de tipo Neumann. En esta charla de divulgación veremos cómo a lo largo del tiempo se ha determinado esta nueva restricción al problema mediante algunos subespacios apropiados de $L^2(\Omega)$. Motivaremos este problema aplicándolo al problema de reconstrucción de imágenes digitales.
TBA
Víctor Nopal
