Primera Escuela Temática en Álgebra y Geometría Algebraica

 

Programa

 

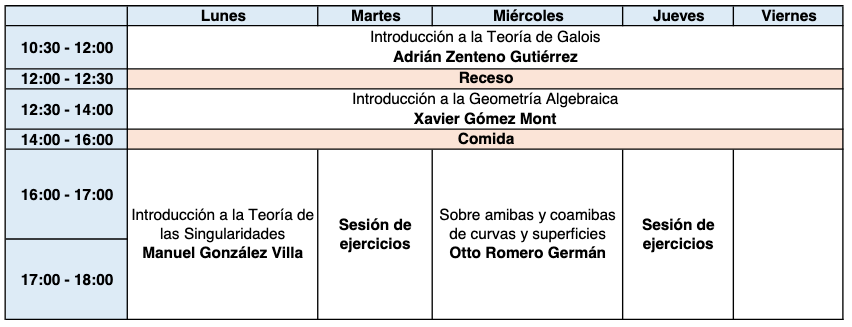
CURSOS

Introducción a la Geometría Algebraica
Por Dr. Xavier Gómez Mont

Que un polinomio en varias variables tiene un “cuerpo geométrico” fue una revelación que nos regaló René Descartes en 1637 al escribir las ecuaciones de las curvas cónicas (círculos, elipses, parábolas, hipérbolas y pares de líneas) como unos polinomios cuadráticos en 2 variables. El tema de la Geometría Algebraica es continuar con este tema, pero en mas de 2 variables, para varios polinomios de grado mayor a 2 y buscar soluciones no solamente sobre los números reales, si no sobre otros campos, como los números racionales o los números complejos.
Iniciaremos el curso describiendo las propiedades de los anillos de polinomios en varias variables y en particular un método contemporáneo que consiste en cambiar los polinomios originales del problema por otros polinomios pero que tienen el mismo conjunto de soluciones. Estas nuevas ecuaciones son o más fáciles de resolver o exhiben a la vista más claramente las propiedades del conjunto definido por ellas.
Posteriormente veremos algunos resultados que den idea de la descripción geométrica y topológica de estos conjuntos que tienen una definición algebraica sencilla.

 

Introducción a la Teoría de Galois
Por Dr. Adrián Zenteno Gutiérrez

Saber si es posible encontrar fórmulas generales para resolver ecuaciones algebraicas, ha sido uno de los problemas que más ha intrigado a los matemáticos a lo largo de la historia. Quizá, el caso más famoso, es la fórmula general para obtener las raíces de un polinomio cuadrático en una variable conocida por los Babilónicos. Fórmulas similares para resolver ecuaciones polinomiales de grado tres y cuatro fueron desarrolladas por Cardano y Ferrari desde el siglo XVI. Sin embargo, el problema de saber si es posible encontrar una fórmula general para resolver ecuaciones polinomiales de grado cinco como en los casos anteriores (es decir, usando solo sumas, restas, multiplicaciones, divisiones y extracción de raíces) permaneció abierto hasta el siglo XIX, cuando Évariste Galois desarrollo una elegante teoría que permitió convertir este problema de teoría de campos en un problema de teoría de grupos más fácil de resolver.
El objetivo de este curso es presentar una introducción a dicha teoría y su aplicación a la resolubilidad por radicales de ecuaciones algebraicas y la constructibilidad con regla y compás.

 

CONFERENCIAS

Sobre amibas y coamibas de curvas y superficies
Por Otto Romero Germán

Como se mencionó en el resumen del primer minicurso, el "cuerpo geométrico" de una cónica, cúbica o en general de un polinomio en 2 variables sobre los reales R es una curva en el plano R^2. Pero sobre los complejos C, el “cuerpo geométrico” es una curva compleja en C^2. Esto es, una superficie de dimensión real 2 viviendo en un espacio de 4 dimensiones (C^2 es homeomorfo a R^4). Una manera de estudiar esas superficies es por medio de sus amibas y coamibas, que son como "fotos" de la curva, en el caso de la amiba la "foto" vive en el plano R^2, mientras que la coamiba vive en un toro (plano) de dimensión 2, esto es, se pueden visualizar en solo dos dimensiones. Esto se generaliza naturalmente a más dimensiones. Las amibas y coamibas contienen información de la curva original. En la plática revisaremos esas construcciones y veremos algunos ejemplos para curvas y ciertas superficies algebraicas. Además de repasar algunas de sus características.

 

Introducción a la Teoría de las Singularidades
Por Manuel González Villa

Uno de los resultados fundamentales de nuestros cursos de Cálculo Diferencial es el Teorema de la Función Implícita, que nos da condiciones para que un conjunto pueda ser parametrizado por unas variables curvas. Pero este Teorema tiene unas hipótesis sobre el rango de la derivada en un punto, o en el caso más sencillo, que la derivada no se anule.
¿Qué pasa cuando estas hipótesis no se cumplen? Este es el tema de la Teoría de las Singularidades. Esta es una Teoría que se ha desarrollado con velocidad desde mediados del siglo XX, y hoy forma una estructura matemática muy impresionante.
El objetivo de la Conferencia será mencionar algunos de los problemas que se estudian en la Teoría de las Singularidades, y las soluciones que se han dado a estos problemas.

 

FECHAS IMPORTANTES

Se amplía la fecha límite de registro: 27 de noviembre 2022

Nota: Si te registras antes del 20 de noviembre tu resultado se te hará llegar el 24 de noviembre, si lo haces posteriormente, se te notificará el día 1o de diciembre.