
SOLICITUD DE ADMISIÓN
Fecha límite de registro domingo 23 de marzo
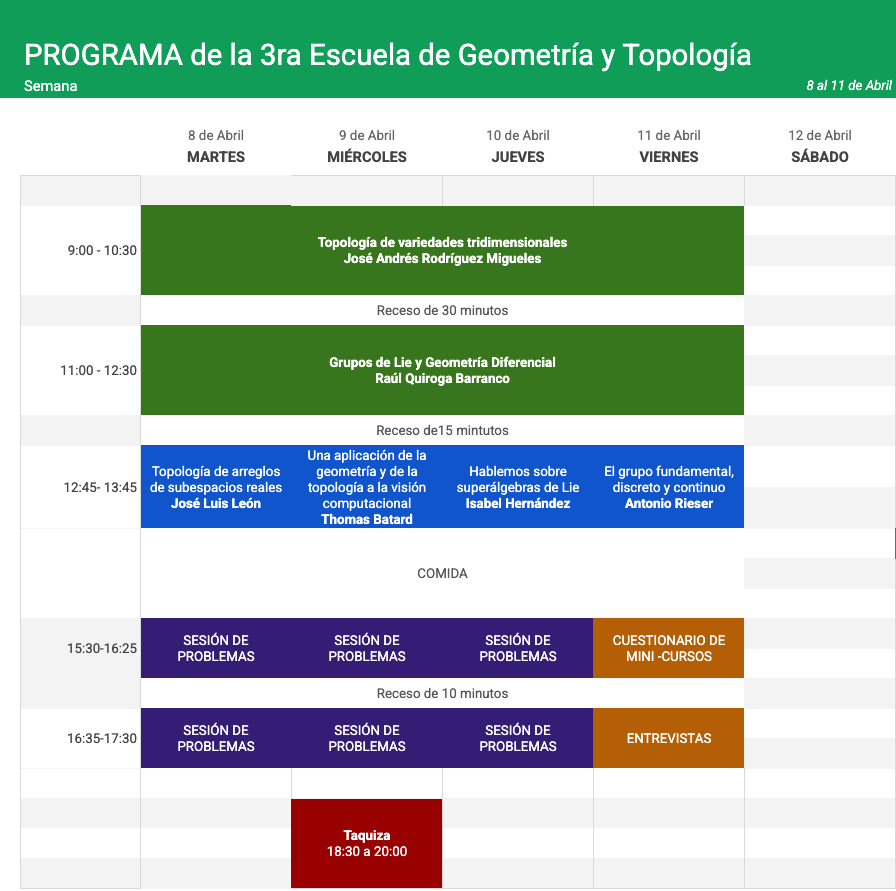
CURSOS
Título: Topología de variedades tridimensionales (minicurso)
José Andrés Rodriguez Migueles
Resumen: El objetivo principal es proporcionar las herramientas necesarias para tener ejemplos concretos de distintas variedades tridimensionales. Los temas que veremos en cada clase serán los siguientes:
- *Construcción de variedades tridimensionales.*
Se estudiará cómo el pegado de variedades de dimensión 3 a lo largo de su su frontera define su topología, y depende únicamente del homeomorfismo de pegado módulo isotopía y conjugación. - *Espacios de identificación de poliedros.*
Exploraremos las estructuras obtenidas mediante identificaciones específicas en poliedros y su relación con la topología de las variedades resultantes. - *La 3-esfera y los cuaternios.*
La 3-esfera se puede identificar con el grupo de cuaternios de norma 1, introducido por William Hamilton. Por esta razón, los cuaterniones aparecen con frecuencia en la topología tridimensional. Analizaremos la conexión entre el álgebra de cuaternios y la geometría. - *El Teorema Fundamental del Dominio. *
Basado en las memorias de Poincaré sobre los grupos fuchsianos, este teorema establece el vínculo entre topología y geometría: Y permite realizar determinadas uniones de poliedros como cocientes de un espacio geométrico modelo entre un grupo discreto de transformaciones isométricas.
Título: Grupos de Lie y Geometría Diferencial
Raúl Quiroga
Resumen: Partimos de dos principios fundamentales en matemáticas. El primero, las simetrías de cualquier objeto matemático se estudia a través de grupos. El segundo, el cálculo diferencial es la base de cualquier estudio matemático de tipo analítico, es decir, propio del análisis matemático. Juntando estos dos hechos, llegamos a los grupos de Lie y sus aplicaciones en geometría. En este mini curso daremos una breve introducción al uso de grupos de Lie en el estudio de espacios Riemannianos. Comenzaremos con las geometrías fundamentales: espacios vectoriales, esferas y espacios hiperbólicos. Veremos entonces cómo los grupos de Lie sirven de guía para intuir y estudiar geometrías más complicadas.
CHARLAS
Título: Topología de arreglos de subespacios reales
José Luis León Medina
Abstract: Se dará una breve introducción a la teoría de arreglos de subespacios reales (colecciones finitas de subespacios afines), resaltando su conexión con varias áreas de las matemáticas. Se mostrarán algunos de sus representantes más conocidos, como los espacios de configuraciones o espacios de no k iguales, y se examinarán qué resultados se tienen acerca de su topología (homotopía) y cómo se pueden entender ciertos funtores homotópicos, como la cohomología sobre esos espacios, por medio de la Dualidad de Poincaré. Finalmente, se verá cómo una adaptación de estos espacios puede aportar información acerca de la expresividad de ciertas redes neuronales.
Título: Hablemos sobre superálgebras de Lie
Ma. Isabel Hernández
Resumen: En esta charla veremos qué son las superálgebras de Lie y sus principales diferencias con las llamadas ''álgebras de Lie". Más específicamente, un espacio vectorial se dice que G-graduado si es un grupo conmutativo que se descompone en suma directa de subespacios etiquetados con los elementos del grupo. En este sentido la palabra ¨súper¨ hace referencia a cuando G=Z_2.
Título: Una aplicación de la geometría y de la topología a la visión computacional.
Thomas Batard
Resumen: En esta charla, estudiaremos un método para clasificar automáticamente los objetos digitales 3D según el número de hoyos que tienen. Este método se basa en el teorema de Gauss-Bonnet que establece una relación entre la geometría de una superficie y su topología. Estudiaremos primero el teorema para superficies regulares, y luego su versión discreta para mallas triangulares 3D a partir de la cual podremos desarrollar el algoritmo de clasificación.
Título: El grupo fundamental, discreto y continuo.
Antonio Rieser
Resumen: Damos una introducción a las propiedades del grupo fundamental en complejos CW y mostramos cómo se puede extender esta construcción a espacios métricos finitos que poseen una escala destacada, como la que se encuentra en el análisis topológico de datos.

