Sexta Escuela Temática en Análisis y Sistemas Dinámicos
04 al 07 de junio 2024
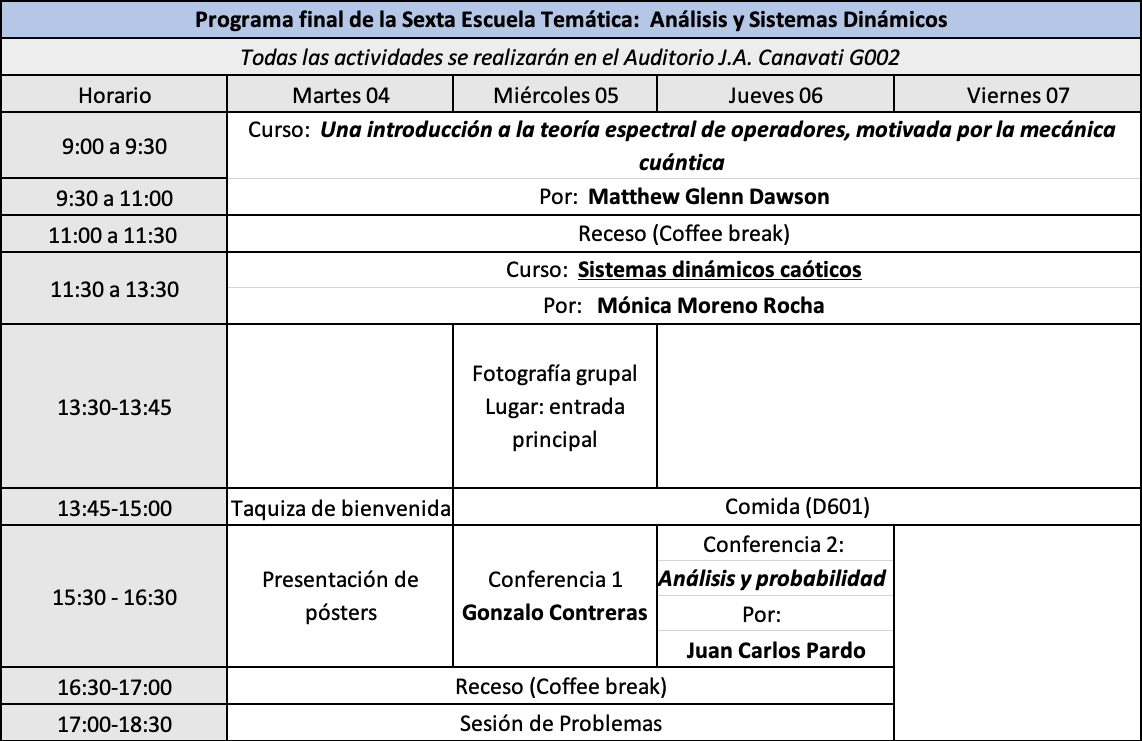
Programa
CURSOS
Una introducción a la teoría espectral de operadores, motivada por la mecánica cuántica
Por: Matthew Glenn Dawson
Resumen: Solemos aprender en un curso de álgebra lineal que las matrices simétricas (con entradas reales) inducen bases ortonormales de vectores propios. Estas diagonalizaciones son una herramienta muy poderosa que nos permiten entender y manipular las matrices con mayor facilidad. Sin embargo, muchas veces es necesario trabajar con transformaciones lineales entre espacios vectoriales de dimensión infinita. Las "diagonalizaciones" de tales operadores se llaman descomposiciones espectrales, y el teorema espectral garantiza que cada operador autoadjunto sobre un espacio de Hilbert admite una descomposición espectral. El teorema espectral tiene muchas aplicaciones a la teoría de ecuaciones diferenciales parciales lineales y a la mecánica cuántica. De hecho, fue el desarrollo reciente de la mecánica cuántica lo que motivó a John von Neumann a formular y demostrar el teorema espectral. En este minicurso, usaremos la mecánica cuántica para motivar e introducir la teoría espectral de operadores autoadjuntos no necesariamente acotados. No es necesario haber trabajado antes con espacios de Hilbert, ya que veremos las definiciones y resultados necesarios sobre el camino, y no es necesario haber estudiado física.
Sistemas dinámicos caóticos
Por: Mónica Moreno Rocha
Resumen: Si has llevado un curso de ecuaciones diferenciales, es posible que asocies el caos a esa propiedad en la que, dadas dos condiciones iniciales cercanas, las soluciones que inician en esos valores tienen en el futuro comportamientos muy distintos. Esta propiedad conocida como “dependencia a condiciones iniciales” es sólo una parte de la definición de caos. El objetivo principal de este curso es entender este concepto desde el enfoque de los sistemas dinámicos y la topología, el análisis y la probabilidad. Estudiaremos también algunos de los mecanismos que producen comportamientos caóticos y discutiremos algunas de las preguntas abiertas de mayor relevancia en la teoría de los sistemas dinámicos caóticos
FECHAS IMPORTANTES
Fecha límite de registro: lunes 27 de mayo
CONTACTO
