SOLICITUD DE ADMISIÓN          ·          FOTO DE GRUPO

 

Programa

 

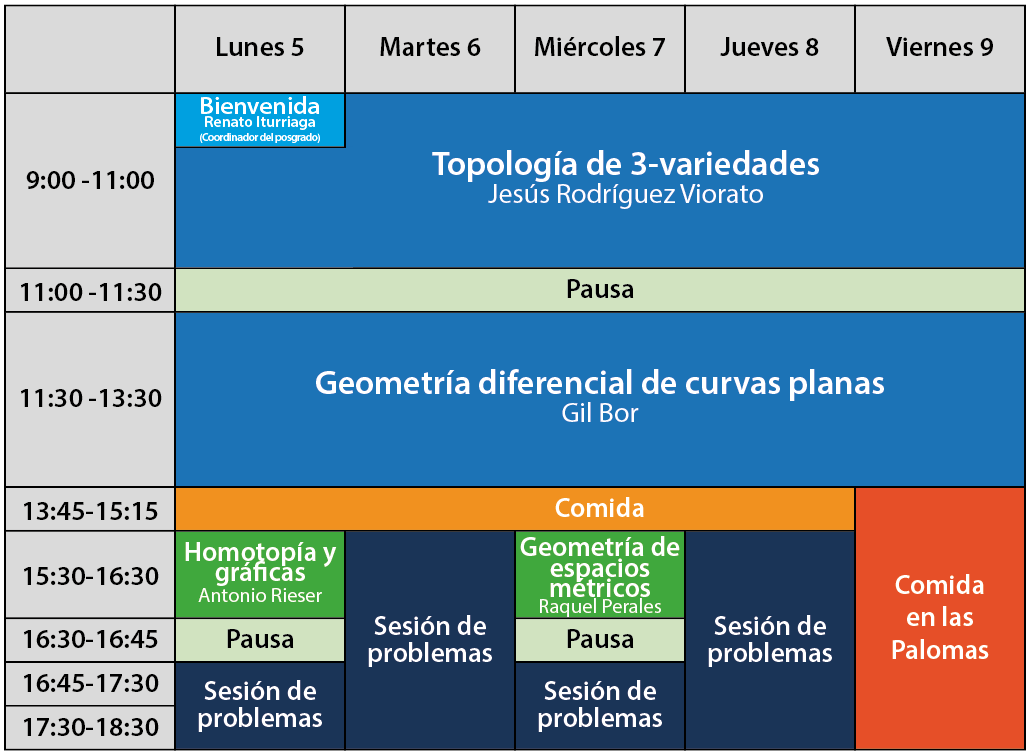
CURSOS

Geometría diferencial de curvas en el plano
Por Dr. Gil Bor

Este curso es una introducción a la geometría diferencial con pocas definiciones y muchos ejemplos y resultados bonitos: el teorema de los 4 vértices, Tait-Kneser, dualidad proyectiva, la involuta y evoluta, trayectorias de bicicletas, las curvas clásicas (la braquistócrona, catenaria, tractriz,…).

 

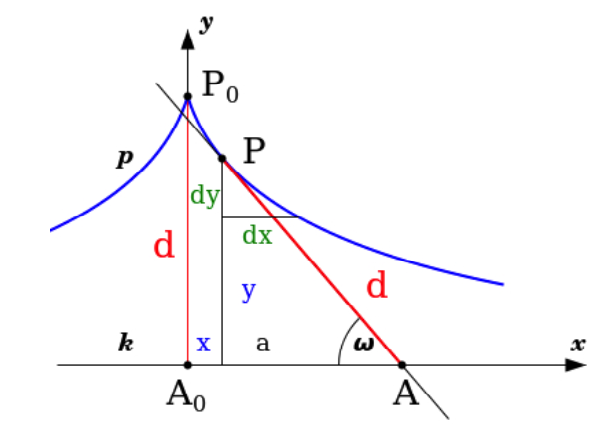
Prerrequisitos: para poder seguir este curso es necesario manejar el material de cálculo vectorial (ie cálculo de varias variables), además de curiosidad y una mente abierta para ideas nuevas.

Referencias:

* https://www.2dcurves.com/
* Hilbert, Cohn-Vossen, Geometry and the Imagination
* Courant & John, Introducción al cálculo y análisis matemático, vol II, cap. 3.

 

 

Topología de las 3-variedades
Por Dr. Jesús Rodríguez Viorato

En este mini-curso estudiaremos variedades topológicas de dimensión 3. Estos objetos han sido ampliamente estudiados desde hace ya más de cien años y se han logrado grandes avances en ellos como la prueba de G. Perelman de la conjetura de Poincaré. El área de las matemáticas que trabaja con 3-variedades se llama Topología en Dimensión Baja; además de las 3-variedades se estudian otros objetos de baja dimensión como son los nudos, superficies y hasta 4-variedades.

Iniciaremos revisando el caso 2-dimensional (el teorema de clasificación de Superficies) y brincaremos a dimensión 3 donde probaremos varios teoremas de descomposición de 3-variedades como suma de factores primos, la descomposición JSJ y el Teorema de Lickorish-Wallace sobre cirugías.

Prerrequisitos: Haber tomado un curso de Topología, en especial conocer la propiedad universal de la topología cociente (Repasar el capítulo de topología cociente de [M]; ver pdf)

[M] Introduction to Topology Class Notes General Topology Topology, 2nd Edition, James R. Munkres: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://faculty.etsu.edu/gardnerr/5357/notes/Munkres-22.pdf

 

CONFERENCIAS

Conferencia 1. Homotopía y gráficas.
Por Dr. Antonio Rieser

 

 

Conferencia 2. Geometría de espacios métricos.
Por  Dra. Raquel Perales

 

 

FECHAS IMPORTANTES

Fecha límite de registro: 14 de mayo